初心に戻って１

一面ヒガンバナに囲まれている柴犬です。10月初旬のサリオパーク祖父江でのワンショットです。

概要

自分の孫の小学生に、コンピューターの整数、特に負の整数をどうしたらうまく説明できるのか、初心に戻って考えてみました。

正しいのか分かりませんが、こうすればいいのではと取り合えずの考えがまとまりましたので、書きます。

まず10 進法で

コンピュータは２進法ですが、ここでは分かりやすく 10 進法で説明します。

まず、３桁の 基数10 の補数を考えます。３桁の繰り上がった数 1000 となりますので、２つの整数をたして 1000 になる整数が互いの補数になるという関係になります。

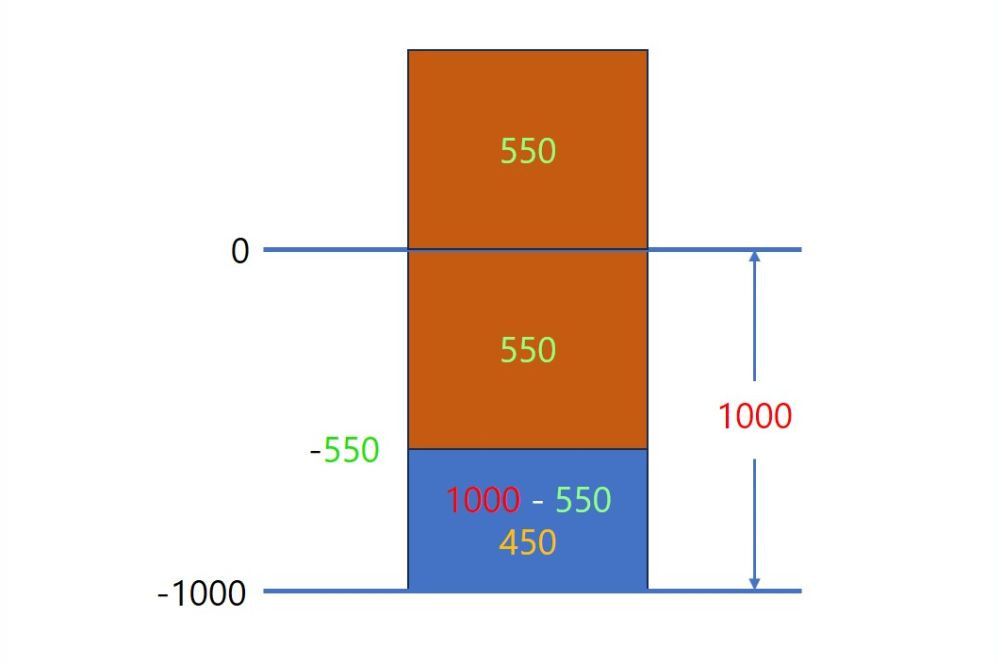
例えば 550 の補数を求めてみます。1000から引くので、補数は 1000 – 550 の 450 となります。

コンピュータの負の整数の表現は、与えられた整数（ここでは 999 まで）の負の値の表現は、与えられた整数の補数の頭に負記号 1（-1000）を付けた表現を負の値としています。

つまり、与えられた整数 550 の負の値（-550）の表現は補数 450 の頭に負記号 1（-1000）を付けた数 1450 が負の表現（実値 -550 ）になります。

ですので、負の整数の実の値は、先頭の 1 は実値 -1000 とし 1450 は -1000 + 450 と計算します。また、与えられた整数 550 はコンピュータの規則で表すなら、先頭に 0 を付けて 0550 と表されます。

逆に、負の整数の表現が 1450 の場合の補数は、1000 – 450 = 550 で、正の表現 0 を付けて 0550 と求められます。

そして、1450 + 0550 は、-1000（負の表現 1 ） + 450 + 0（正の表現 0 ） + 550 → -1000 + 450 + 550 = 0 となります。

図にまとめると次のようになります。

2 進法

同様にして 2 進法では8 ビットの場合、 7 桁の補数を考えます。例えば、0110011 の補数は 7 桁から繰り上がった数 10000000 から引いた 1001101 が補数となります。この頭に負記号 1（10000000=-128）を付けた数 11001101 が負の表現となります。

ですので、11111111 は　10000000 = -128、1111111=127 なので 11111111=-128+127=-1 となります。

実践

孫にはまだ実践していませんが、機会があればこの説明をしたいと思います。

その実践の結果で補足・修正が生じれば、今後編集します。

弊社はメッセナゴヤ2023に出展いたします。心よりご来場をお待ちしております。